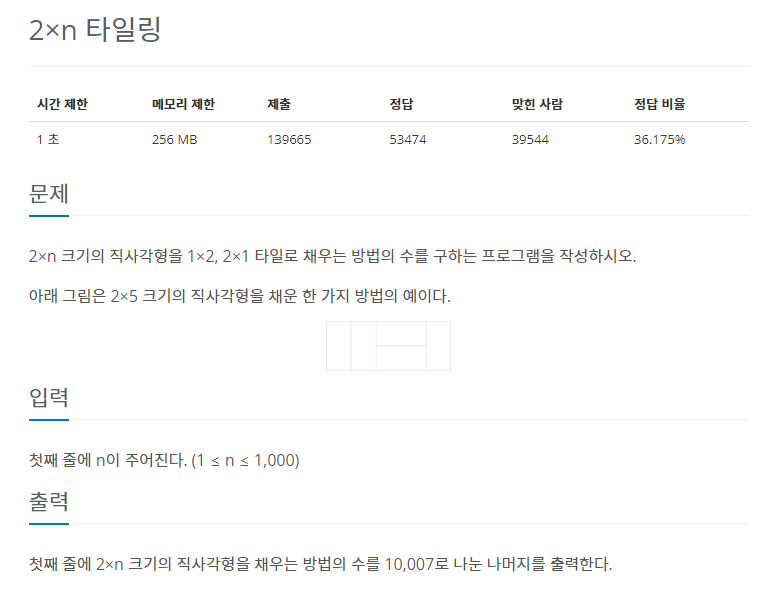
2*1 타일 또는 1*2 타일로 2*N 정사각형을 채우는 방법의 수를 찾는 문제입니다.
– 먼저 상태와 종료 조건을 생각해보자. => 상태 N, 종료 조건: ?
변경되지 않는 것: 각 2*N 타일을 채우는 방법의 수, 예를 들어 2*2 타일을 채우는 경우, 2*1은 나란히, 1*2는 위와 아래, 2를 채우는 방법의 수, etc. 2*N 타일 2*N-1 ….2*1 을 채우는 경우의 수를 찾는 과정에서 생성되는 경우의 수는 변하지 않습니다.
이제 큰 문제를 작은 문제로 나누어 보겠습니다.
2*N 타일을 채우는 과정에서 2*n-1 ..2*n-2.. 2*n-3 타일을 채우는 경우의 수가 변하지 않으면 사용할 수 있다.
2*N-1 타일에서 2*1 타일 하나 추가모양이 2*N 타일인 경우 2*N을 채우는 방법의 수는 2*n-1을 채우는 방법의 수와 같습니다.
예를 들어 2*3을 만드는 방법의 수가 2*2 + 2*1 타일 하나인 경우 2*2를 만드는 방법의 수와 2*3을 만드는 방법의 수가 중요한 것이지 수가 아닙니다. 같을 것이다
또한 2*N 타일은 2*N-2 타일에서 2개의 1*2 타일을 추가합니다.하나의 모양에 대해 2*N을 채우는 방법의 수는 2*N-2 타일을 추가하는 방법의 수와 같습니다.
예를 들어, 2*3을 만드는 방법의 수가 2*1에 1*2를 두 개 더하면 2*3을 만드는 방법의 수는 2*1을 만드는 방법의 수와 같습니다.
따라서 하나의 2*N-1 타일 2*1 타일을 추가하여 2*N 타일을 만들거나 두 개의 1*2 타일을 위아래로 2*N-2 타일로 추가하여 2*N 타일을 만듭니다. 2*N-1을 만드는 경우의 수는 2*N-2를 만드는 경우의 수에 2*N-2를 만드는 경우의 수를 더한 것과 같습니다.
재귀 공식 D(N) = D(N-1) + D(N-2)
종료 조건: 2*0 타일을 만드는 방법은 여러 가지이므로 0을 반환하고, 2*1 타일을 만드는 방법은 한 가지뿐이므로 1을 반환합니다.
2*2 타일을 만드는 방법은 2가지이므로 2 반환
public class Main {
public static int() d;
public static void main(String() args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
d = new int(n+1);
d(1)=1;
System.out.print(two_n(n));
}
public static int two_n(int n){
if(n == 0) return 0;
if(n == 2) return 2;
if(d(n) > 0) return d(n);
d(n) = two_n(n-1) + two_n(n-2);
d(n) %= 10007;
return d(n);
}
}결과를 10007로 나눈 값을 반환하라고해서 나눴습니다.
d(2) = 2가 저장되고 시작되지 않으면 n = 1일 때 예외가 발생합니다.

