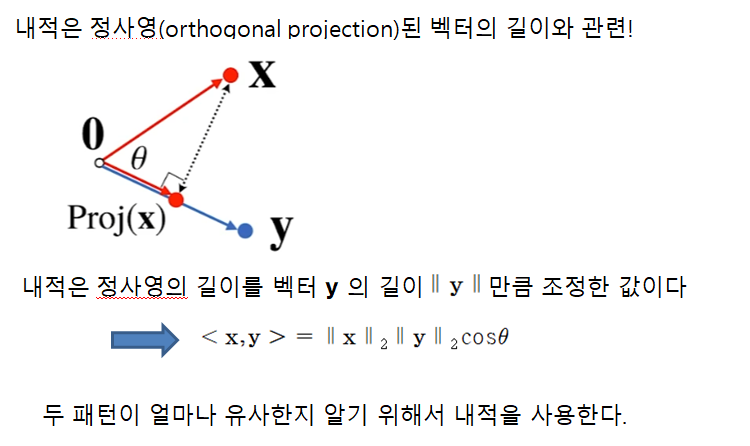
(이 강의를 통해 잘 몰랐거나 새로 알게 된 내용을 정리했습니다.)
벡터 사이 같은 모양있다면 Hadamard 제품을 계산할 수 있습니다.
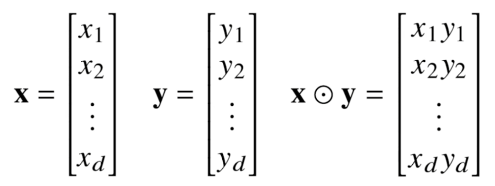
1):
import numpy as np
2)에서:
x = np.array((1, 7, 2))
y = np.array((5, 2, 1))
3시에):
x+y
끄기(3):
array((6, 9, 3))(4)에서:
x-y
끄기(4):
array((-4, 5, 1))(6)에서:
x * y
밖으로 (6):
array(( 5, 14, 2))
기준
벡터의 노름은 원점으로부터의 거리말한다
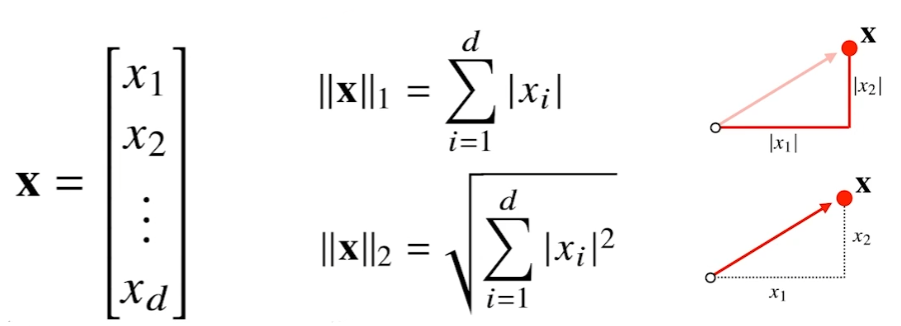
x의 L1 규범: 각 구성 요소의 변화에 대한 모든 절댓값을 더합니다.
x의 L2 놈: 피타고라스 정리를 사용하여 유클리드 거리를 계산합니다.
규범은 임의의 차원입니다 디끝났다는 것을 기억하자!!
서로 다른 유형의 규범에는 서로 다른 기하학적 속성이 있습니다!
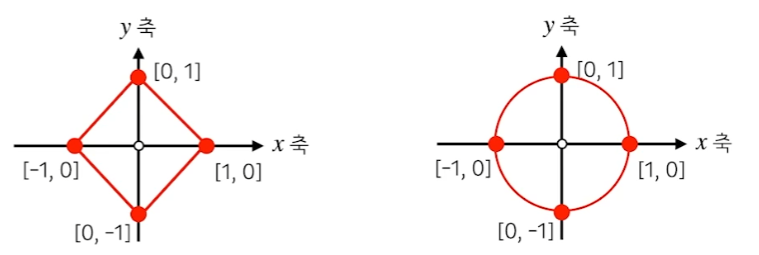

L1 규범: 강력한 학습, lasso 회귀에 사용됨 L2 규범: 라플라스 근사,
릿지 회귀에 사용
(7)에서:
def l1_norm(x):
x_norm = np.abs(x)
x_norm = np.sum(x_norm)
return x_norm
def l2_norm(x):
x_norm = x*x
x_norm = np.sum(x_norm)
x_norm = np.sqrt(x_norm)
return x_norm
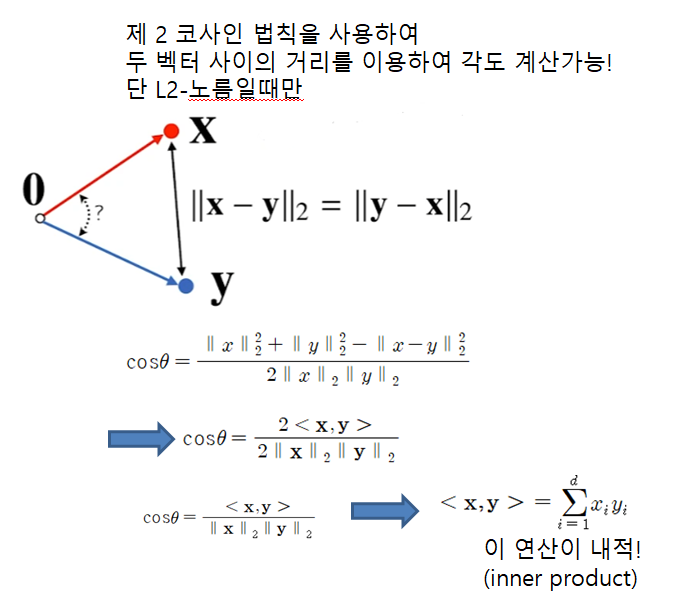
8시에):
def angle(x,y):
v = np.inner(x,y) / (l2_norm(x) * l2_norm(y))
tehta = np.arccos(v)
return theta